Advertisements
Advertisements
Question
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.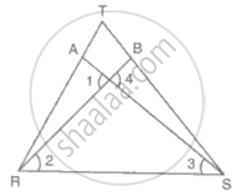
Solution
∠1 = 2∠2 and ∠4 = 2∠3
1 = 22 and 4 = 23∠1 = ∠4 ...(vertically opposite angles)
⇒ 2∠2 = 2∠3 or ∠2 = ∠3 ........(i)
∠R = ∠S = ...(since RT = TS and angle opposite to equal sides are equal)
⇒ ∠TRB = ∠TSA = .........(ii)
In ΔRBT and ΔSAT.
RT = TS
∠TRB = ∠TSA
∠RTB = ∠STA = ...(common)
Therefore, ΔRBT ≅ ΔSAT. ...(ASA criteria)
APPEARS IN
RELATED QUESTIONS
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
If ΔABC ≅ ΔABC is isosceles with
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
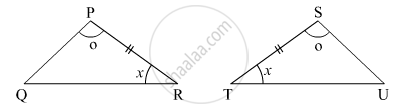
By ______ test
ΔPRQ ≅ ΔSTU
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.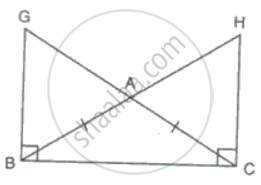
Prove that
(i) BG = CH
(ii) AG = AH
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
