Advertisements
Advertisements
Question
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.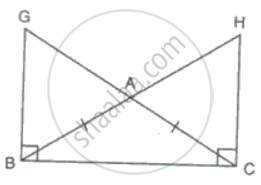
Prove that
(i) BG = CH
(ii) AG = AH
Solution
In ΔABC
AB = AC
∠ABC = ∠ACB ...(equal sides have equal angles opposite to them)...(i)
∠GBC = ∠HCB = 90° ........(ii)
Subtracting (i) from (ii)
∠GBA = ∠HCA..........(iii)
In ΔGBA and ΔHCA
∠GBA = ∠HCA ...(from iii)
∠BAG - ∠CAH ...(vertically opposite angles)
BC = BC
Therefore, ΔGBA ≅ ΔHCA ...(ASA criteria)
Hence, BG = CH and AG = AH.
APPEARS IN
RELATED QUESTIONS
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
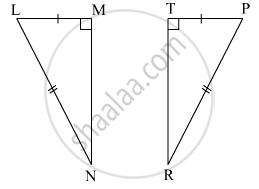
By ______ test
ΔLMN ≅ ΔPTR
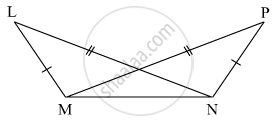
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
If the following pair of the triangle is congruent? state the condition of congruency :
In ΔABC and ΔDEF, ∠B = ∠E = 90o; AC = DF and BC = EF.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC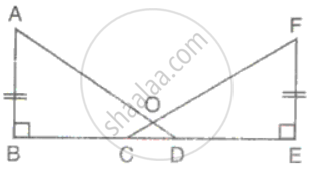
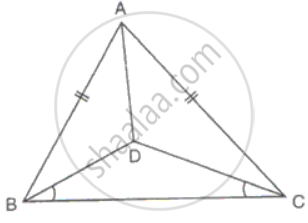
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.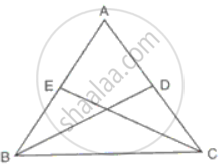
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.