Advertisements
Advertisements
प्रश्न
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.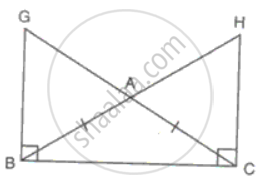
Prove that
(i) BG = CH
(ii) AG = AH
उत्तर
In ΔABC
AB = AC
∠ABC = ∠ACB ...(equal sides have equal angles opposite to them)...(i)
∠GBC = ∠HCB = 90° ........(ii)
Subtracting (i) from (ii)
∠GBA = ∠HCA..........(iii)
In ΔGBA and ΔHCA
∠GBA = ∠HCA ...(from iii)
∠BAG - ∠CAH ...(vertically opposite angles)
BC = BC
Therefore, ΔGBA ≅ ΔHCA ...(ASA criteria)
Hence, BG = CH and AG = AH.
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
In triangles ABC and PQR three equality relations between some parts are as follows:
AB = QP, ∠B = ∠P and BC = PR
State which of the congruence conditions applies:
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
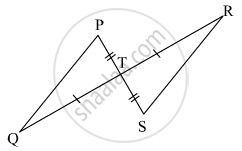
From the information shown in the figure,
in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...[Vertically opposite angles]
∴ ΔPTQ ≅ ΔSTR ...`square` test
∴ `{:("∠TPQ" ≅ square),("and" square ≅ "∠TRS"):}}` ...corresponding angles of congruent triangles
seg PQ ≅ `square` ...corresponding sides of congruent triangles
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
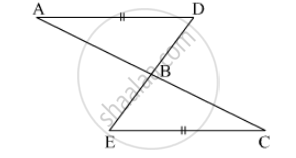
State, whether the pairs of triangles given in the following figures are congruent or not:

In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
