Advertisements
Advertisements
प्रश्न
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
विकल्प
PQ < TP
PQ < TQ
TQ < TP < PQ
PQ < TP < TQ
उत्तर
PQ < TQ
Explanation:
∠Q = 180° – (95° + 65°)
∠Q = 20°
∴ ∠Q < ∠T < ∠P
∴ PT < PQ < TQ
APPEARS IN
संबंधित प्रश्न
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(EF)`
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
In ΔPQR ≅ ΔEFD then ED =
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
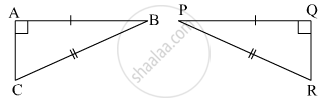
State, whether the pairs of triangles given in the following figures are congruent or not:

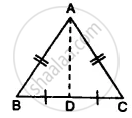
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
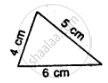
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
