Advertisements
Advertisements
प्रश्न
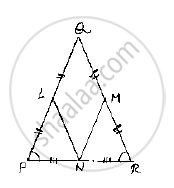
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
उत्तर
Given that, in PQR, PQ QRand L,M,N are midpoints of the sides PQ, QP and RP
respectively and given to prove that LN MN
Here we can observe that PQR is and isosceles triangle
⇒PQ =QR and ∠QPR =∠QRP ……..(1)
And also, L and M are midpoints of PQ and QR respectively
⇒ `PL=LQ=(PQ)/2,QM=MR=(QR)/2`
And also, PQ=QR
⇒ `PL=LQ=QM=MR=(PQ)/2=(QR)/2` .............(2)
Now, consider ΔLPN and ,Δ MRN
LP= MR [From – (2)]
∠LPN =∠MRN [From – (1)]
∵∠QPR and ∠LPN and ∠ QRP and ∠MRN are same
PN= NR [∵N is midpoint of PR]
So, by SAS congruence criterion, we have LPN≅ MRN
⇒LN =MN
[ ∵Corresponding parts of congruent triangles are equal]
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
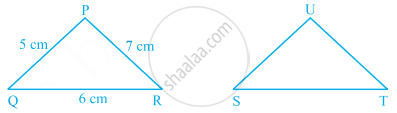
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?
The top and bottom faces of a kaleidoscope are congruent.
