Advertisements
Advertisements
Question
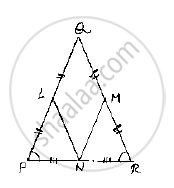
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
Solution
Given that, in PQR, PQ QRand L,M,N are midpoints of the sides PQ, QP and RP
respectively and given to prove that LN MN
Here we can observe that PQR is and isosceles triangle
⇒PQ =QR and ∠QPR =∠QRP ……..(1)
And also, L and M are midpoints of PQ and QR respectively
⇒ `PL=LQ=(PQ)/2,QM=MR=(QR)/2`
And also, PQ=QR
⇒ `PL=LQ=QM=MR=(PQ)/2=(QR)/2` .............(2)
Now, consider ΔLPN and ,Δ MRN
LP= MR [From – (2)]
∠LPN =∠MRN [From – (1)]
∵∠QPR and ∠LPN and ∠ QRP and ∠MRN are same
PN= NR [∵N is midpoint of PR]
So, by SAS congruence criterion, we have LPN≅ MRN
⇒LN =MN
[ ∵Corresponding parts of congruent triangles are equal]
APPEARS IN
RELATED QUESTIONS
Mark the correct alternative in each of the following:
If ABC ≅ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
If ΔABC ≅ ΔABC is isosceles with
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.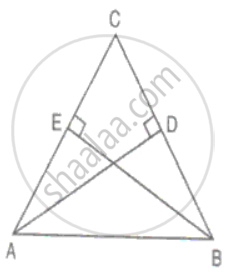
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.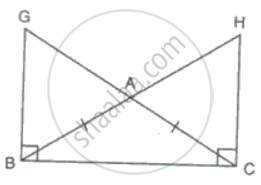
Prove that
(i) BG = CH
(ii) AG = AH
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles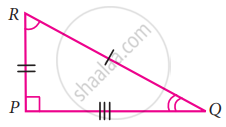

In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
