Advertisements
Advertisements
Question
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
Solution
Given:
ABCD is a parallelogram, where BE = CE
To prove:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
a. In ΔDCE and ΔLBE
∠DCE = ∠EBL ....[DC || AB, alternate angles]
CE = BE ....[given]
∠DEC = ∠LEB ....[vertically opposite angles]
∴ By Angle-Side-Angle criterion of congruence,
ΔDCE ≅ ΔLBE
The corresponding parts of the congruent triangles are congruent.
∴ DC = LB ....(1)
b. DC = AB ....(2)[opposite sides of a parallelogram]
From (1) and (2),
AB = BL ....(3)
c. Al = AB + BL
⇒ AL = Ab + AB ....[From (3)]
⇒ AL = 2AB
⇒ Al = 2DC. ....[From (2)]
APPEARS IN
RELATED QUESTIONS
Find the measure of each angle of an equilateral triangle.
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
If ΔPQR≅ ΔEFD, then ∠E =
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
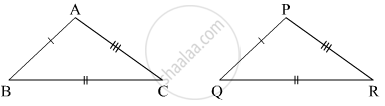
By ______ test
Δ ABC ≅ ΔPQR
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent angles
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
