Advertisements
Advertisements
Question
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent angles
Solution
Given ∆ABC ≅ ∆DEF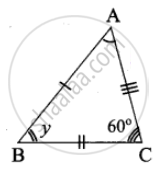
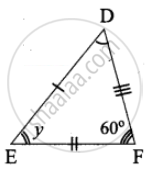
Corresponding congruent angles.
∠ABC = ∠DEF, ∠BCA = ∠EFD, ∠CAB = ∠FDE
APPEARS IN
RELATED QUESTIONS
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In ΔPQR ≅ ΔEFD then ED =
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
By ______ test
Δ ABC ≅ ΔPQR
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
State, whether the pairs of triangles given in the following figures are congruent or not:

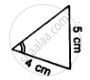
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.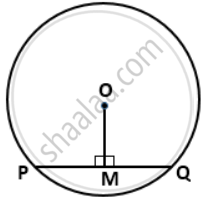
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.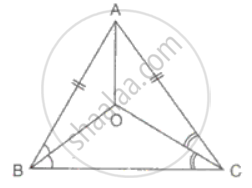
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.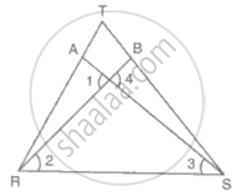
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.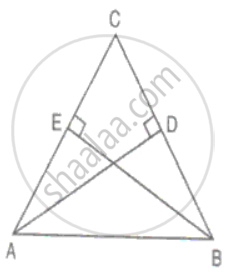
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
