Advertisements
Advertisements
Question
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.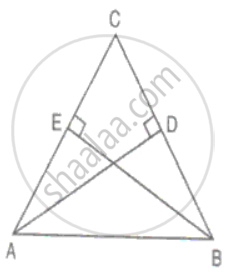
Solution
In ΔCAD and ΔCBE
CA = CB ...(Isosceles triangles)
∠CDA = ∠CEB = 90°
∠ACD = ∠BCE = ...(common)
Therefore, ΔCAD ≅ ΔCBE ...(AAS criteria)
Hence, CE = CD
But, CA = CB
⇒ AE + CE = BD + CD
⇒ AE = BD.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
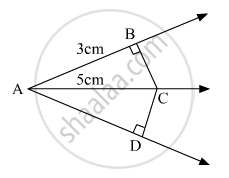
In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
