Advertisements
Advertisements
प्रश्न
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.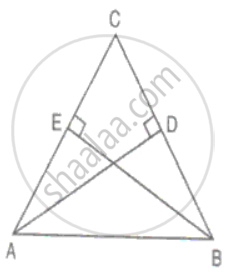
उत्तर
In ΔCAD and ΔCBE
CA = CB ...(Isosceles triangles)
∠CDA = ∠CEB = 90°
∠ACD = ∠BCE = ...(common)
Therefore, ΔCAD ≅ ΔCBE ...(AAS criteria)
Hence, CE = CD
But, CA = CB
⇒ AE + CE = BD + CD
⇒ AE = BD.
APPEARS IN
संबंधित प्रश्न
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
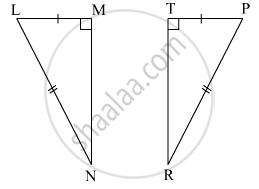
By ______ test
ΔLMN ≅ ΔPTR
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

State, whether the pairs of triangles given in the following figures are congruent or not:
Δ ABC in which AB = 2 cm, BC = 3.5 cm and ∠C = 80° and Δ DEF in which DE = 2 cm, DF = 3.5 cm and ∠D = 80°.
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.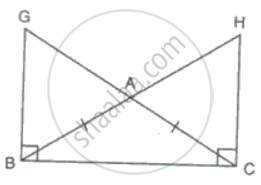
Prove that
(i) BG = CH
(ii) AG = AH
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent angles
If AB = QR, BC = PR and CA = PQ, then ______.
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
