Advertisements
Advertisements
प्रश्न
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.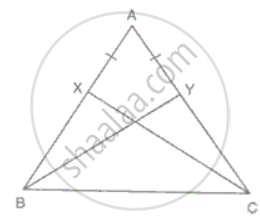
उत्तर
In ΔABC
AB = AC
AX = AY
⇒ BX = CY
In ΔBXC and ΔCYB
BX = CY
BC = BC
∠B = ∠C = C ...(AB = AC and angles opposite to equal sides are equal)
Therefore, ΔBXC ≅ ΔCYB ...(SAS criteria)
Hence, CX = BY.
APPEARS IN
संबंधित प्रश्न
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
In ΔPQR ≅ ΔEFD then ED =
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
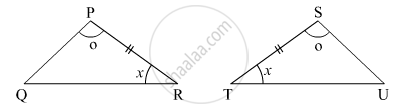
By ______ test
ΔPRQ ≅ ΔSTU
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
State, whether the pairs of triangles given in the following figures are congruent or not:

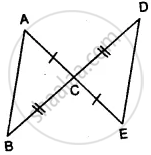
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.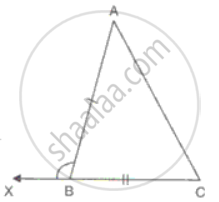
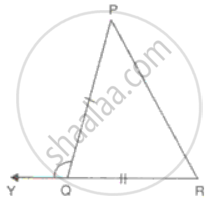
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
The top and bottom faces of a kaleidoscope are congruent.
