Advertisements
Advertisements
प्रश्न
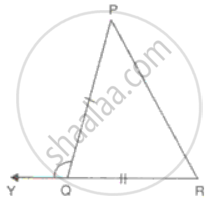
In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.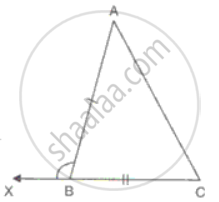
उत्तर
In ΔABC and ΔPQR and
AB = PQ
BC = QR
∠ABX + ∠ABC
= ∠PQY + ∠PQR
= 180°
∠ABX = ∠PQY
⇒ ∠ABC = ∠PQR
Therefore,
ΔABC ≅ΔPQR ....(SAS criteria).
APPEARS IN
संबंधित प्रश्न
In triangles ABC and PQR three equality relations between some parts are as follows:
AB = QP, ∠B = ∠P and BC = PR
State which of the congruence conditions applies:
State, whether the pairs of triangles given in the following figures are congruent or not:

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.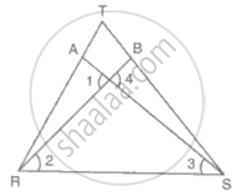
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
If AB = QR, BC = PR and CA = PQ, then ______.
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
