Advertisements
Advertisements
प्रश्न
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
उत्तर
Given:
D os mid-point of BC
⇒ BD = DC
DE = AD
To prove:
a. ΔABD ≅ ΔECD
b. AB = EC
c. AB || EC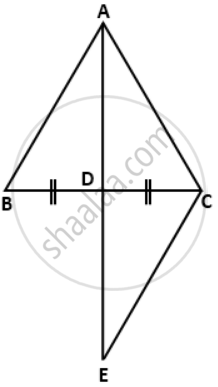
a. In ΔABD and ΔECD
BD = DC ....(given)
∠ADB = ∠CDE ....(vertically opposite angles)
AD = DE ....(given)
∴ By Side-Angle-Side criterion of congruence,
ΔABD ≅ ΔECD
b. The corresponding parts of the congruent triangle are congruent.
∴ AB = EC
c. Also, ∠DAB = ∠DEC ....(c.p.c.t)
∴ AB || EC ....(∠DAB and ∠DEC are alternate angles).
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(BC = 5cm,AC = 6cm,∠C = 80°);
ΔXYZ;(XZ = 6cm,XY = 5cm,∠X = 70°).
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.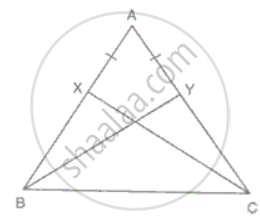
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
The top and bottom faces of a kaleidoscope are congruent.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆STU ≅ ∆DEF
