Advertisements
Advertisements
प्रश्न
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
उत्तर
Given:
D os mid-point of BC
⇒ BD = DC
DE = AD
To prove:
a. ΔABD ≅ ΔECD
b. AB = EC
c. AB || EC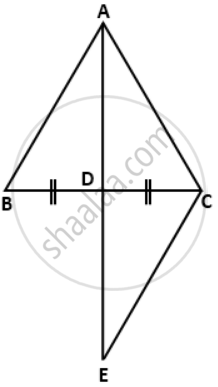
a. In ΔABD and ΔECD
BD = DC ....(given)
∠ADB = ∠CDE ....(vertically opposite angles)
AD = DE ....(given)
∴ By Side-Angle-Side criterion of congruence,
ΔABD ≅ ΔECD
b. The corresponding parts of the congruent triangle are congruent.
∴ AB = EC
c. Also, ∠DAB = ∠DEC ....(c.p.c.t)
∴ AB || EC ....(∠DAB and ∠DEC are alternate angles).
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
In a squared sheet, draw two triangles of equal areas such that
The triangles are not congruent.
What can you say about their perimeters?
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
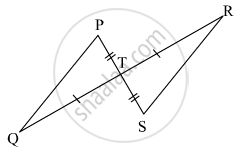
From the information shown in the figure,
in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...[Vertically opposite angles]
∴ ΔPTQ ≅ ΔSTR ...`square` test
∴ `{:("∠TPQ" ≅ square),("and" square ≅ "∠TRS"):}}` ...corresponding angles of congruent triangles
seg PQ ≅ `square` ...corresponding sides of congruent triangles
In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.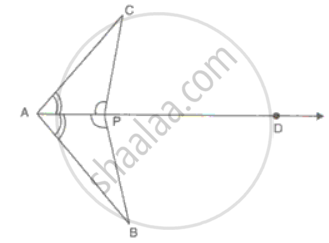
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC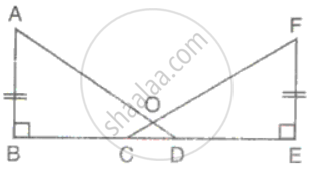
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.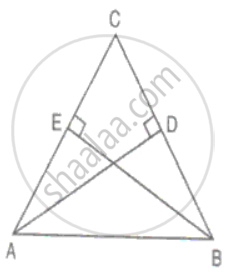
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
In the given figure, AB = DB and AC = DC. Find the values of x and y.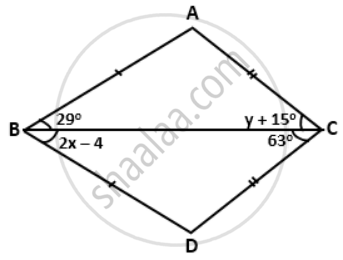
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
