Advertisements
Advertisements
प्रश्न
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
उत्तर
No, we know that two triangles are congruent, if the sides and angles of one triangle are equal to the corresponding side and angles of other triangle.
Here ΔABC ≅ ΔRPQ
AB = RP, BC = PQ and AC = RQ
Hence, it is not true to say that BC = QR.
APPEARS IN
संबंधित प्रश्न
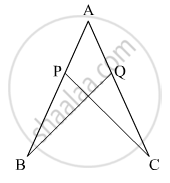
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

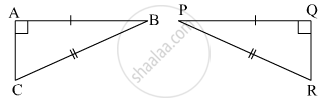
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
State, whether the pairs of triangles given in the following figures are congruent or not:
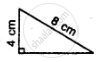
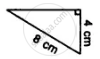
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.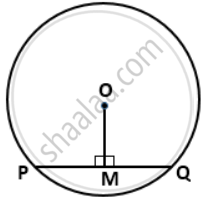
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
Which of the following rule is not sufficient to verify the congruency of two triangles
If AB = QR, BC = PR and CA = PQ, then ______.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
