Advertisements
Advertisements
प्रश्न
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.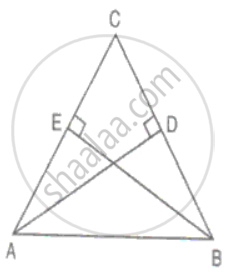
उत्तर
In ΔCAD and ΔCBE
CA = CB ...(Isosceles triangles)
∠CDA = ∠CEB = 90°
∠ACD = ∠BCE = ...(common)
Therefore, ΔCAD ≅ ΔCBE ...(AAS criteria)
Hence, CE = CD
But, CA = CB
⇒ AE + CE = BD + CD
⇒ AE = BD.
APPEARS IN
संबंधित प्रश्न
In a squared sheet, draw two triangles of equal areas such that
The triangles are not congruent.
What can you say about their perimeters?
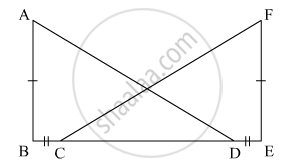
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
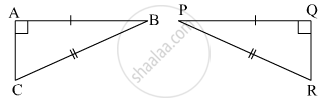
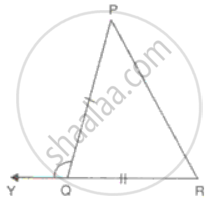
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.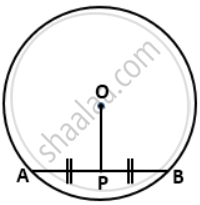
In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.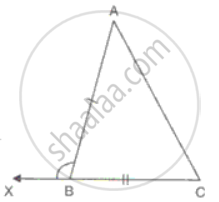
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
Which of the following rule is not sufficient to verify the congruency of two triangles
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆XYZ ≅ ∆MLN
