Advertisements
Advertisements
प्रश्न
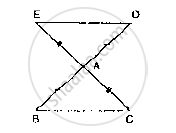
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
उत्तर
In ΔADE and ΔBAC
AE = AC
AB = AD
∠BAD = ∠EAC
∠DAC = ∠DAC = DAC ...(common)
⇒ ∠BAC = ∠EAD = EAD
Therefore, ΔADE ≅ ΔBAC ...(SAS criteria)
Hence, BC = DE.
APPEARS IN
संबंधित प्रश्न
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
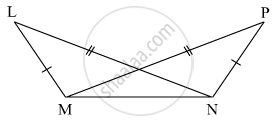
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
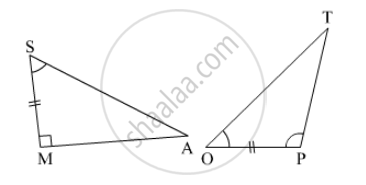
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
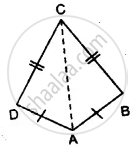
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.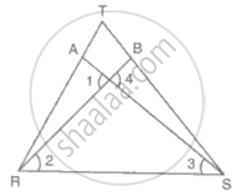
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.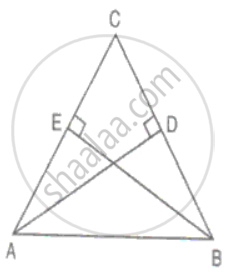
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
