Advertisements
Advertisements
प्रश्न
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
उत्तर
Given:
In ΔPQR,
PA is the perpendicular bisector of QR ⇒ QA = RA
RC is the perpendicular bisector of PQ ⇒ PC = QC
QB is the perpendicular bisector of PR ⇒ PR = RB
PA, RC and QB meet at I.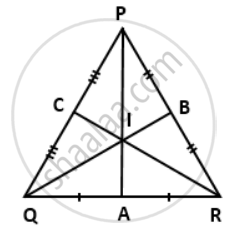
To prove: IP = IQ = IR
Proof:
In ΔQIA and ΔRIA
QA = RA ....[Given]
∠QAI = ∠RAI ....[Each = 90]
IA = IA ....[Common]
∴ By Side-Angle-Side criterion of congruence,
ΔIQ = IR ....(i)
Similarly, in ΔRIB and ΔPIB
RB = PB ...[Given]
∠RBI = ∠PBI ...[Each = 90°]
IB = IB ...[Common]
∴ By Side-Angle-Side criterion of congruence,
ΔRIB ≅ ΔPIB
The corresponding parts of the congruent triangles are congruent.
∴ IR = IP ....(ii)
From (i) and (ii), we have
IP = IQ = IR.
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
In ΔPQR ≅ ΔEFD then ED =
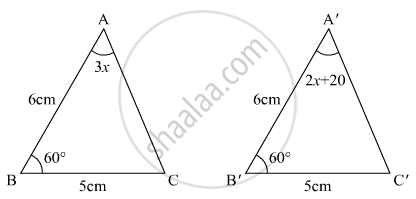
In the given figure, the measure of ∠B'A'C' is
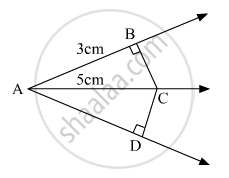
In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
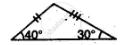
State, whether the pairs of triangles given in the following figures are congruent or not:
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.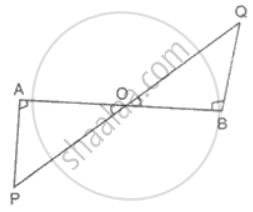
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
