Advertisements
Advertisements
प्रश्न
In the given figure, the measure of ∠B'A'C' is
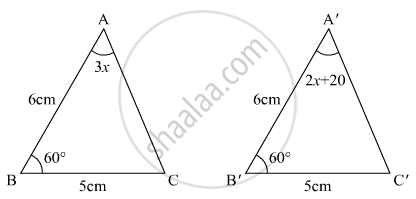
विकल्प
50°
60°
70°
80°
उत्तर
We have to find B’A’C’

ince triangles are congruent
So ∠A = ∠A
3X = 2X + 20
X = 20
Now in A’B’C’
∠A + ∠B + C = 180° (By property of triangle)
60° + 60° + ∠C = 180°
∠C = 60°
∠A = 2X + 20
`= 2 xx 20° + 20°`
= 40° + 20
= 60°
Hence (b) B’A’C’ = 60°.
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
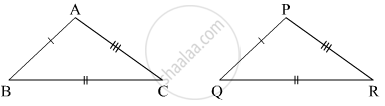
By ______ test
Δ ABC ≅ ΔPQR
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.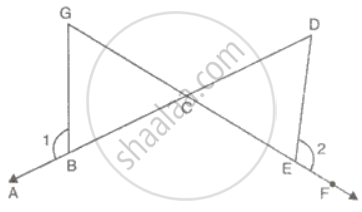
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
