Advertisements
Advertisements
प्रश्न
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
विकल्प
20°
40°
60°
80°
उत्तर
In the triangle ABC it is given that
AB = AC
∠ACD = 100°
We have to find ∠A
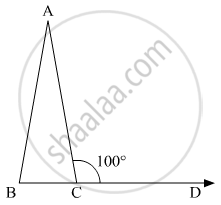
Now ∠ACD + ∠ACB = 180° (linear pair)
SinceAB = AC
So, ∠B = ∠C (by isosceles triangle)
This implies that
∠B =∠C
= 180° - 100
= 80
Now,
∠A + ∠B + ∠C = 180° (Property of triangle)
∠A + 80° + 80° = 180°
∠A = 180° - 160°
∠A = 20°
APPEARS IN
संबंधित प्रश्न
If ΔPQR≅ ΔEFD, then ∠E =
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.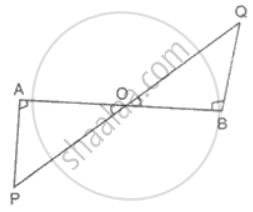
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
