Advertisements
Advertisements
प्रश्न
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.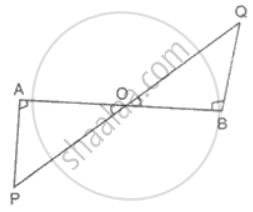
उत्तर
Since AP and BQ are perpendiculars to the line segment AB, therefore Ap and BQ are parallel to each other.
In ΔAOP and ΔBOQ
∠PAQ = ∠QBO = 90°
∠APO = ∠BQO ...(alternate angles)
AP = BQ
Therefore, ΔAOP ≅ ΔBOQ AOP BOQ ...(ASA criteria)
Hence, AO = OB and PO = OQ
Thus, O is the mid-point of the line segments AB and PQ.
APPEARS IN
संबंधित प्रश्न
Find the measure of each angle of an equilateral triangle.
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
In the given figure, prove that: ∆ ABD ≅ ∆ ACD
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.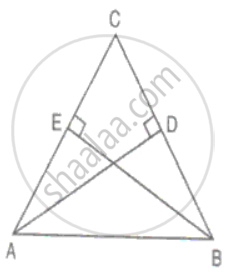
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
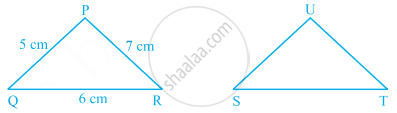
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?