Advertisements
Advertisements
Question
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.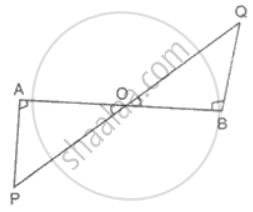
Solution
Since AP and BQ are perpendiculars to the line segment AB, therefore Ap and BQ are parallel to each other.
In ΔAOP and ΔBOQ
∠PAQ = ∠QBO = 90°
∠APO = ∠BQO ...(alternate angles)
AP = BQ
Therefore, ΔAOP ≅ ΔBOQ AOP BOQ ...(ASA criteria)
Hence, AO = OB and PO = OQ
Thus, O is the mid-point of the line segments AB and PQ.
APPEARS IN
RELATED QUESTIONS
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
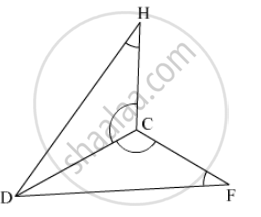
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
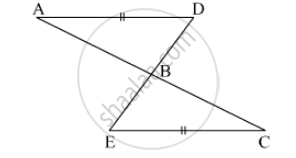
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

State, whether the pairs of triangles given in the following figures are congruent or not:
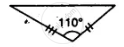
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
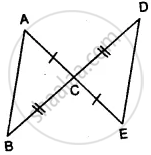
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles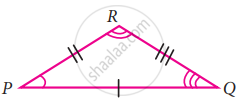
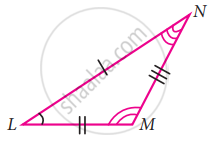
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
