Advertisements
Advertisements
Question
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
Solution
∠BCD = ∠ADC
∠ACB = ∠BDA
∠BCD + ∠ACB = ∠ADC + ∠BDA
⇒ ∠ACD = ∠BDCACD = BDC
In ΔACD and ΔBCD
∠ACD =∠BDCACD = BDC
∠ADC = ∠BCD
ADC = BCD
CD = CD
Therefore, ΔACD ≅ ΔBCD ...(ASA criteria)
Hence, AD = BC and ∠A = ∠B.
APPEARS IN
RELATED QUESTIONS
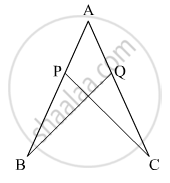
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
Mark the correct alternative in each of the following:
If ABC ≅ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
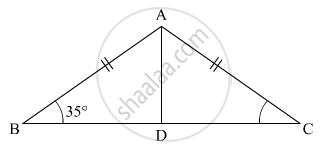
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
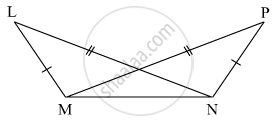
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
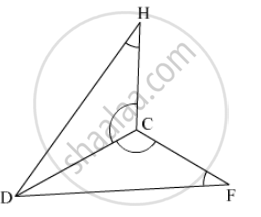
In the given figure, ∠P ≅ ∠R seg, PQ ≅ seg RQ. Prove that, ΔPQT ≅ ΔRQS.

In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.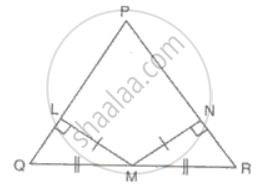
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
If AB = QR, BC = PR and CA = PQ, then ______.
