Advertisements
Advertisements
Question
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
Solution
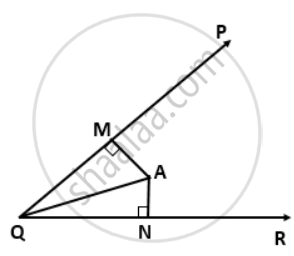
Given,
AM ⊥ PQ and AN ⊥ QR
AM = AN
In ΔAQM and ΔAQN,
AM = AN ....(given)
AQ = AQ ....(common)
∠AMQ - ∠ANQ ....(Each = 90°)
So, by R.H.S. congruence, we have
ΔAQM ≅ ΔAQN
⇒ ∠AQM = ∠AQN ....(c.p.c.t)
⇒ ∠AQP = ∠AQR.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
Find the measure of each angle of an equilateral triangle.
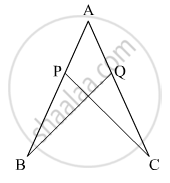
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
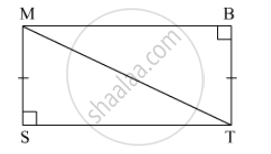
If the following pair of the triangle is congruent? state the condition of congruency :
In ΔABC and ΔDEF, ∠B = ∠E = 90o; AC = DF and BC = EF.
State, whether the pairs of triangles given in the following figures are congruent or not:

Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
