Advertisements
Advertisements
प्रश्न
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
उत्तर
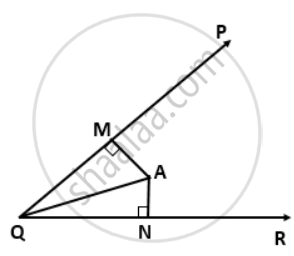
Given,
AM ⊥ PQ and AN ⊥ QR
AM = AN
In ΔAQM and ΔAQN,
AM = AN ....(given)
AQ = AQ ....(common)
∠AMQ - ∠ANQ ....(Each = 90°)
So, by R.H.S. congruence, we have
ΔAQM ≅ ΔAQN
⇒ ∠AQM = ∠AQN ....(c.p.c.t)
⇒ ∠AQP = ∠AQR.
APPEARS IN
संबंधित प्रश्न
Mark the correct alternative in each of the following:
If ABC ≅ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
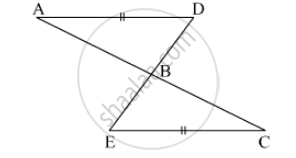
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
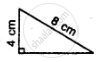
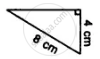
State, whether the pairs of triangles given in the following figures are congruent or not:
In the given figure, prove that: ∆ ABD ≅ ∆ ACD
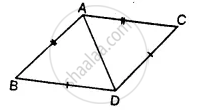
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
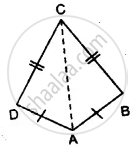
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.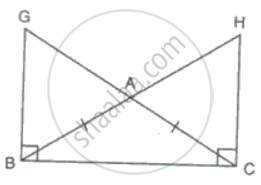
Prove that
(i) BG = CH
(ii) AG = AH
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Which of the following rule is not sufficient to verify the congruency of two triangles
