Advertisements
Advertisements
प्रश्न
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
उत्तर
∠PQT = ∠RQU .....(i)
∠TQS = ∠UQS .....(ii)
Adding (i) and (ii)
∠PQS = ∠RQS
In ΔPQS and ΔRQS
∠PQS = ∠RQS
PQ = RQ ...(given)
QS = QS ...(common)
Therefore, ΔPQS ≅ ΔRQS ...(SAS criteria)
Hence, ∠QPS = ∠QRS
Now in ΔPQT and ΔRQU
∠QPS = ∠QRS
PQ = RQ ...(given)
∠PQT = ∠RQU ...(given)
Therefore, ΔPQT ≅ ΔRQU ...ASA criteria)
Hence, QT =QU.
APPEARS IN
संबंधित प्रश्न
Mark the correct alternative in each of the following:
If ABC ≅ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
Prove that:
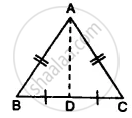
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
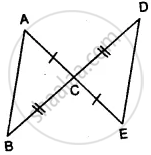
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(BC = 5cm,AC = 6cm,∠C = 80°);
ΔXYZ;(XZ = 6cm,XY = 5cm,∠X = 70°).
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.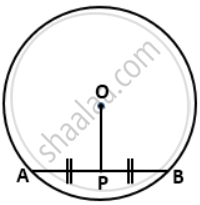
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.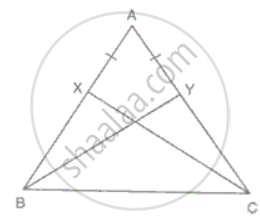
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆STU ≅ ∆DEF
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
