Advertisements
Advertisements
प्रश्न
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
उत्तर
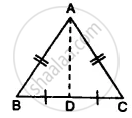
Given: In the figure,
AB = AC
BD = CD
To prove:
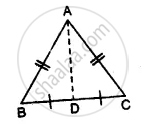
- Δ ABD ≅ Δ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
Proof: In Δ ABD and Δ ACD
AD = AD ...(common)
AB = AC ...(given)
BD = CD ...(given)
(i) ∴ Δ ABD ≅ Δ ACD ...(SSS axiom)
(ii) ∴ ∠B = ∠C ...(c.p.c.t.)
(iii) ∠ADB = ∠ADC ...(c.p.c.t.)
But ∠ADB + ∠ADC = 180° ...(Linear pair)
∴ ∠ADB = ∠ADC
(iv) ∠ADB = ∠ADC
= `(180°)/2`
= 90°
APPEARS IN
संबंधित प्रश्न
Find the measure of each angle of an equilateral triangle.
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
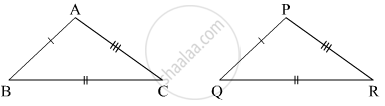
By ______ test
Δ ABC ≅ ΔPQR
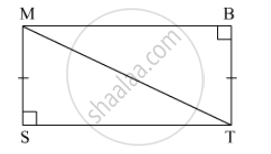
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
State, whether the pairs of triangles given in the following figures are congruent or not:
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.
Which of the following rule is not sufficient to verify the congruency of two triangles
