Advertisements
Advertisements
प्रश्न
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
उत्तर
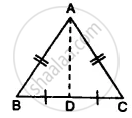
Given: In the figure,
AB = AC
BD = CD
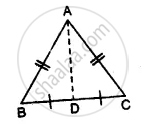
To prove:
- Δ ABD ≅ Δ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
Proof: In Δ ABD and Δ ACD
AD = AD ...(common)
AB = AC ...(given)
BD = CD ...(given)
(i) ∴ Δ ABD ≅ Δ ACD ...(SSS axiom)
(ii) ∴ ∠B = ∠C ...(c.p.c.t.)
(iii) ∠ADB = ∠ADC ...(c.p.c.t.)
But ∠ADB + ∠ADC = 180° ...(Linear pair)
∴ ∠ADB = ∠ADC
(iv) ∠ADB = ∠ADC
= `(180°)/2`
= 90°
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
State, whether the pairs of triangles given in the following figures are congruent or not:

In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.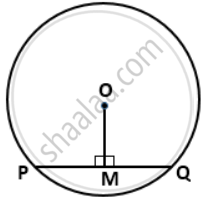
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.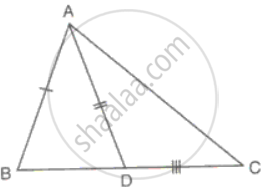
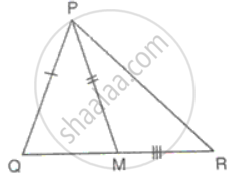
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
