Advertisements
Advertisements
प्रश्न
Prove that:
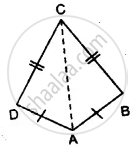
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
उत्तर
Given: In the figure,
AB = AD, CB = CD
To prove: Δ ABC ≅ Δ ADC
∠B = ∠D
AC bisects angle DCB
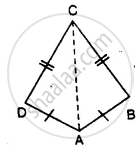
Proof: In Δ ABC and Δ ADC,
AC = AC .............(common)
AB = AD .............(given)
CB = CD .............(given)
(i) ∴ Δ ABC ≅ Δ ADC .................(SSS aciom)
(ii) ∴ ∠B = D .................(c.p.c.t.)
∠BCA = ∠DCA
(iii) ∴ AC bisects ∠DCB
APPEARS IN
संबंधित प्रश्न
In a squared sheet, draw two triangles of equal areas such that
The triangles are not congruent.
What can you say about their perimeters?
If ΔABC ≅ ΔABC is isosceles with
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
In the given figure, prove that: ∆ ABD ≅ ∆ ACD
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC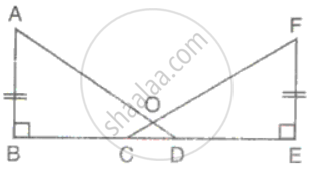
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.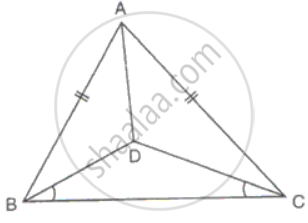
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
