Advertisements
Advertisements
प्रश्न
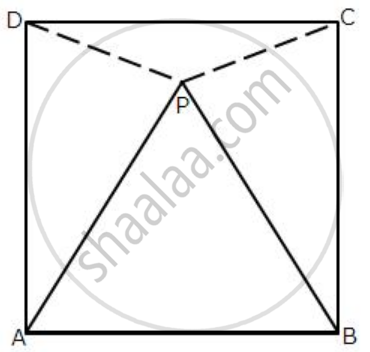
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
उत्तर
Given: ABCD is a Square and ΔAPB is an equilateral triangle.
We need to
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC
Proof:
Since AB side is present in both square & equilateral triangle
AP = PB = AB =AD = CD = BC
(i) In ΔBPC,
BP = BC
∴ ∠BPC = ∠PCB
∠BPC + ∠PCB + 30° = 180°
∠BPC + ∠BPC = 150°
2∠BPC = ` (150°)/2 = 75°`
∴ ∠BPC = ∠PCB = 75°
∠ADP = ∠DPA = 75° ...[C.P.C.T.C]
(ii) In DPC
∠DCP = 90° - 75° = 15°
∠PDC = 90° - 75° = 15°
∠DPC = 180° - (15° + 15°)
∠DPC = 150°
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.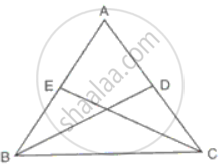
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
