Advertisements
Advertisements
प्रश्न
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
उत्तर
Given: ΔABD is an equilateral triangle.
ΔACE is an equilateral triangle
We need to prove that
(i) ∠CAD = ∠BAE

Proof:
(i) ΔABD is equilateral
∴ Each angle = 60°
⇒ ∠BAD = 60° ...(1)
Similarly,
ΔACE is equilateral
∴ Each angle = 60°
⇒ ∠CAE = 60° ...(2)
⇒ ∠BAD = ∠CAE ...[ from (1) and (2) ]...(3)
Adding ∠BAC to both sides, we have
⇒ ∠BAD + ∠BAC = ∠CAE + ∠BAC
⇒ ∠CAD = ∠BAE ...(4)
(ii) In ΔCAD and ΔBAE
AC = AE ...[ ΔACE is equilateral]
∠CAD = ∠BAE ... [ from (4) ]
AD = AB ...[ ΔABD is equilateral]
∴ By the Side-Angle-Side criterion of congruency,
ΔCAD ≅ ΔBAE
The corresponding parts of the congruent
triangles are congruent.
∴ CD = BE ...[ by c.p.c.t ]
Hence proved.
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
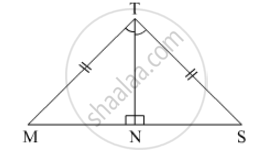
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
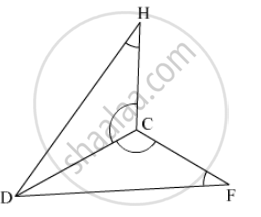
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.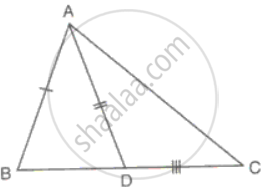
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
