Advertisements
Advertisements
Question
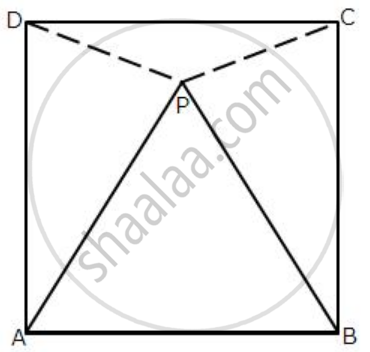
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
Solution
Given: ABCD is a Square and ΔAPB is an equilateral triangle.
We need to
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC
Proof:
Since AB side is present in both square & equilateral triangle
AP = PB = AB =AD = CD = BC
(i) In ΔBPC,
BP = BC
∴ ∠BPC = ∠PCB
∠BPC + ∠PCB + 30° = 180°
∠BPC + ∠BPC = 150°
2∠BPC = ` (150°)/2 = 75°`
∴ ∠BPC = ∠PCB = 75°
∠ADP = ∠DPA = 75° ...[C.P.C.T.C]
(ii) In DPC
∠DCP = 90° - 75° = 15°
∠PDC = 90° - 75° = 15°
∠DPC = 180° - (15° + 15°)
∠DPC = 150°
APPEARS IN
RELATED QUESTIONS
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
Find the measure of each angle of an equilateral triangle.
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
Which of the following is not a criterion for congruence of triangles?
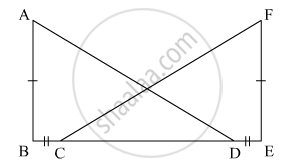
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 5cm,BC = 7cm,CA = 9cm);
ΔKLM;(KL = 7cm,LM = 5cm,KM = 9cm).
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
The top and bottom faces of a kaleidoscope are congruent.
