Advertisements
Advertisements
Question
The top and bottom faces of a kaleidoscope are congruent.
Options
True
False
Solution
This statement is True.
Explanation:
Because they superimpose each other.
APPEARS IN
RELATED QUESTIONS
Complete the congruence statement:
ΔBCA ≅?
ΔQRS ≅?
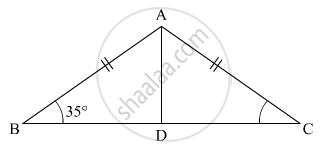
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

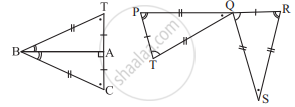
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
By ______ test
Δ ABC ≅ ΔPQR
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) AM = AN (ii) ΔAMC ≅ ΔANB

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
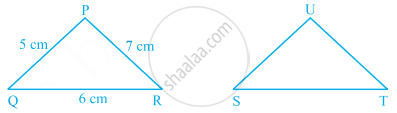
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?