Advertisements
Advertisements
Question
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
Solution

In ΔBXD and ΔCYD
∠BXD = ∠CYD ...(90)
∠XDB = ∠YDC ...(vertically opposite angles)
BD = DC ...(AD is median on BC)
Therefore, ΔBXD ≅ ΔCYD ...(AAS criteria)
Hence, BX = CY.
APPEARS IN
RELATED QUESTIONS
Find the measure of each angle of an equilateral triangle.
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
In the given figure, ∠P ≅ ∠R seg, PQ ≅ seg RQ. Prove that, ΔPQT ≅ ΔRQS.

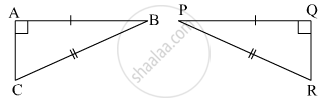
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent angles
Two figures are congruent, if they have the same shape.
