Advertisements
Advertisements
Question
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
Solution
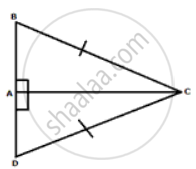
In ΔABC and ΔADC
∠BAC = ∠DAC ...(90°)
BC = DC
AC = AC ...(common)
Therefore, ΔABC ≅ ΔADC ...(SSA criteria)
Hence, ∠BCA = ∠DCA
Thus, AC bisects ∠BCD.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(EF)`
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
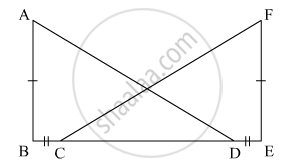
If the following pair of the triangle is congruent? state the condition of congruency :
In ΔABC and ΔDEF, ∠B = ∠E = 90o; AC = DF and BC = EF.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

State, whether the pairs of triangles given in the following figures are congruent or not:
Δ ABC in which AB = 2 cm, BC = 3.5 cm and ∠C = 80° and Δ DEF in which DE = 2 cm, DF = 3.5 cm and ∠D = 80°.
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.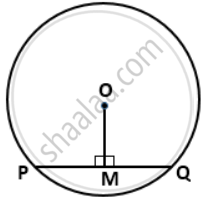
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.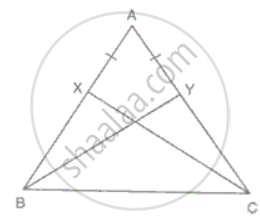
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
The top and bottom faces of a kaleidoscope are congruent.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
