Advertisements
Advertisements
Question
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.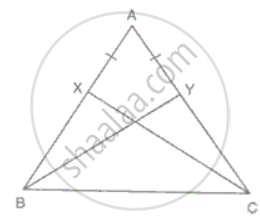
Solution
In ΔABC
AB = AC
AX = AY
⇒ BX = CY
In ΔBXC and ΔCYB
BX = CY
BC = BC
∠B = ∠C = C ...(AB = AC and angles opposite to equal sides are equal)
Therefore, ΔBXC ≅ ΔCYB ...(SAS criteria)
Hence, CX = BY.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
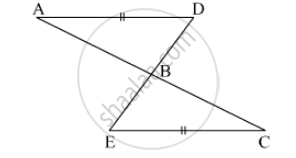
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.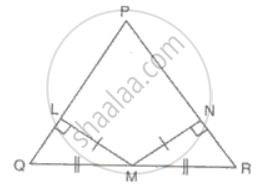
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
Which of the following rule is not sufficient to verify the congruency of two triangles
The top and bottom faces of a kaleidoscope are congruent.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
