Advertisements
Advertisements
Question
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
Solution
Given:
In the figure, OA=OC, AB =BC
We need to prove that,
AOB = 90°
(i) In ΔABO and ΔCBO,
AB = BC ...[given ]
AO = CO ...[ given ]
OB = OB ...[ common ]
∴By Side-Side-Side criterion of congruence, we have
ΔABO ≅ ΔCBO
The corresponding parts of the congruent triangles are congruent.
∴∠ABO = ∠CBO ...[c. p.c.t. ]
⇒ ∠ABD = ∠CBD
and ∠AOB = ∠COB ...[c. p.c t ]
We have
∠AOB + ∠COB = 180° .....[ linear pair ]
⇒ ∠AOB = ∠ COB= 90° and AC ⊥ BD
(ii) In ΔAOD and ΔCOD,
OD = OD ...[ common ]
∠AOD = ∠COD ...[ each=90° ]
AO = CO ...[ given]
∴By Side-Angel-Side criterion of congruence, we have
ΔAOD ≅ ΔCOD
(iii) The corresponding parts of the congruent
triangles are congruent.
∴AD = CD ...[c. p.c t ]
Hence proved.
APPEARS IN
RELATED QUESTIONS
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
Which of the following is not a criterion for congruence of triangles?
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
In the given figure, ∠P ≅ ∠R seg, PQ ≅ seg RQ. Prove that, ΔPQT ≅ ΔRQS.

In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC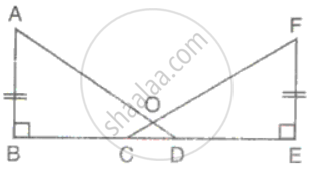
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
Which of the following rule is not sufficient to verify the congruency of two triangles
