Advertisements
Advertisements
Question
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
Solution
In the figure, AP and BQ are equal and parallel to each other.
∴ AP = BQ and AP || BQ.
We need to prove that
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other
(i) ∵ AP || BQ
∴∠APO =∠BOQ ...[ Alternate angles ] ...(1)
and ∠PAO =∠QBO ...[ Alternate angles ] ...(2)
Now in ΔAOP and ΔBOQ.
∠APO =∠BQO ...[ from (1) ]
AP = BQ ...[ given ]
∠PAO = ∠QBO ...[ from (1) ]
∴ By Angel-Side-Angel criterion of congruence, we have
ΔAOP≅ ΔBOQ.
(ii) The corresponding parts of the congruent triangles are congruent.
∴ OP = OQ ...[ c. p. c .t ]
OA = OB ...[ c. p. c .t ]
Hence AB and PQ bisect each other.
APPEARS IN
RELATED QUESTIONS
In a squared sheet, draw two triangles of equal areas such that
The triangles are congruent.
What can you say about their perimeters?
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
State, whether the pairs of triangles given in the following figures are congruent or not:

In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.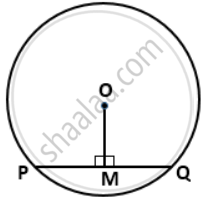
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
