Advertisements
Advertisements
Question
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
Solution
In ΔBMR and DNR
BM = DN
∠BMR = ∠DNR = 90°
∠BRM = ∠DRN = ...(vertically opposite angles)
Hence, ∠MBR = ∠NDR ...(sum of angles of a triangle = 180°)
ΔBMR ≅ ΔDNR ...(ASR criteria)
Therefore, BR = DR
So, AC bisects BD.
APPEARS IN
RELATED QUESTIONS
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
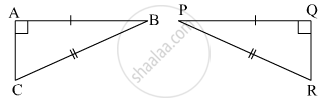
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles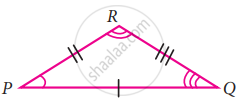
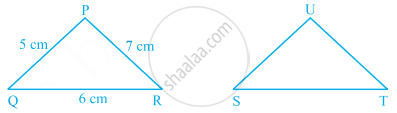
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?
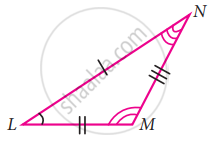
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
