Advertisements
Advertisements
प्रश्न
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
उत्तर
In ΔBMR and DNR
BM = DN
∠BMR = ∠DNR = 90°
∠BRM = ∠DRN = ...(vertically opposite angles)
Hence, ∠MBR = ∠NDR ...(sum of angles of a triangle = 180°)
ΔBMR ≅ ΔDNR ...(ASR criteria)
Therefore, BR = DR
So, AC bisects BD.
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
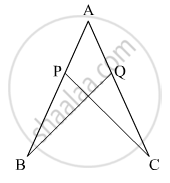
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
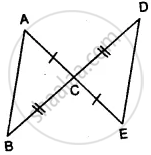
State, whether the pairs of triangles given in the following figures are congruent or not:

In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.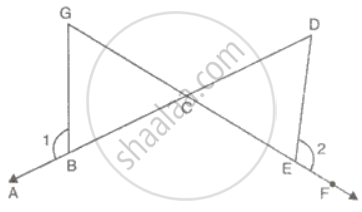
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.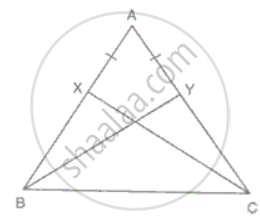
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
