Advertisements
Advertisements
प्रश्न
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.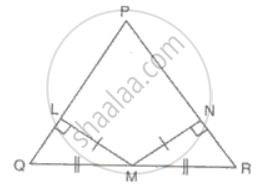
उत्तर
In ΔQLM and ΔRNM
QM = MR
LM = MN
∠QLM = ∠RNM = 90°
Therefore, ΔQLM ≅ ΔRNM ...(RHS criteria)
Hence, QL = RN ..........(i)
Join PM
In ΔPLM and ΔPNM and
PM = PM ...(common)
LM = MN
∠PLM = ∠PNM = 90°
Therefore, ΔPLM ≅ ΔPNM ...(RHS criteria)
Hence, PL = PN ..........(ii)
From (i) and (ii)
PQ = PR.
APPEARS IN
संबंधित प्रश्न
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
Which of the following is not a criterion for congruence of triangles?
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
In the given figure, ∠P ≅ ∠R seg, PQ ≅ seg RQ. Prove that, ΔPQT ≅ ΔRQS.

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
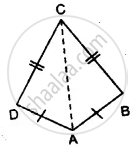
In the following figure, OA = OC and AB = BC.

Prove that: AD = CD
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.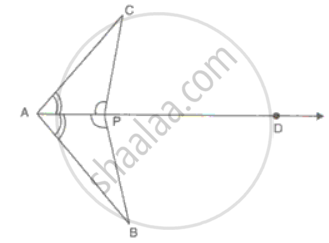
The congruent figures super impose each other completely.
