Advertisements
Advertisements
Question
In a squared sheet, draw two triangles of equal areas such that
The triangles are congruent.
What can you say about their perimeters?
Solution
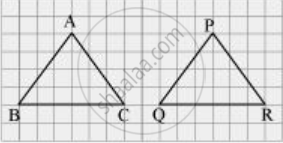
Here, ΔABC and ΔPQR have the same area and are congruent to each other also. Also, the perimeter of both the triangles will be the same.
APPEARS IN
RELATED QUESTIONS
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
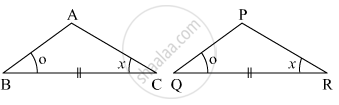
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the given figure P is a midpoint of chord AB of the circle O. prove that OP ^ AB.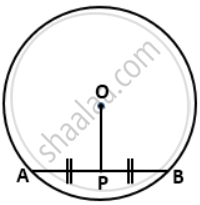
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.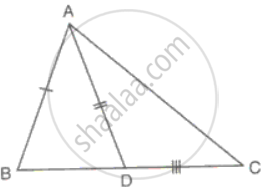
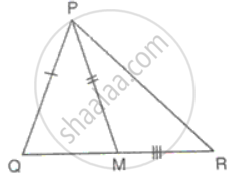
Which of the following rule is not sufficient to verify the congruency of two triangles
The congruent figures super impose each other completely.
