Advertisements
Advertisements
Question
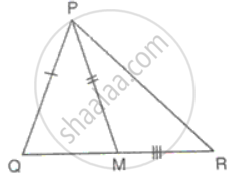
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.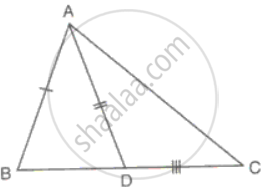
Solution
In ΔABC and ΔPQR
BC = QR
AD and PM are medians of BC and QR respectively
⇒ BD = DC = QM = MR
In ΔABD and ΔPQM
AB = PQ
D = PM
BD = QM
Therefore, ΔABD ≅ ΔPQMABD PQM ...(SSS criteria)
Hence, ∠B = ∠Q
Now in ΔABC and ΔPQR
AB = PQ
BC = QR
∠B = ∠Q
Therefore, ΔABC ≅ ΔPQRABC PQR. ...(SAS criteria)
APPEARS IN
RELATED QUESTIONS
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
In the given figure, ∠P ≅ ∠R seg, PQ ≅ seg RQ. Prove that, ΔPQT ≅ ΔRQS.

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(BC = 5cm,AC = 6cm,∠C = 80°);
ΔXYZ;(XZ = 6cm,XY = 5cm,∠X = 70°).
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
In the given figure, AB = DB and AC = DC. Find the values of x and y.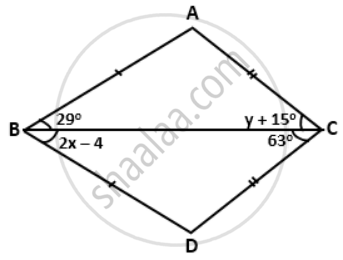
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
The top and bottom faces of a kaleidoscope are congruent.
