Advertisements
Advertisements
Question
In a squared sheet, draw two triangles of equal areas such that
The triangles are not congruent.
What can you say about their perimeters?
Solution
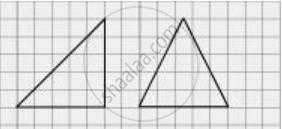
Here, the two triangles have the same height and base. Thus, their areas are equal. However, these triangles are not congruent to each other. Also, the perimeter of both the triangles will not be the same.
APPEARS IN
RELATED QUESTIONS
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
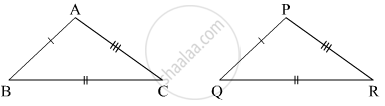
By ______ test
Δ ABC ≅ ΔPQR
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
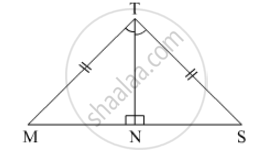
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
State, whether the pairs of triangles given in the following figures are congruent or not:

Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.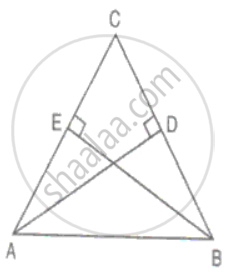
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆STU ≅ ∆DEF
