Advertisements
Advertisements
Question
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

Options
5 cm
6 cm
7 cm
8 cm
Solution
In the following figure we are given
DY = 3cm
AZ = 2cm
Where ABCD is a square and AXYZ is also a square
We are asked to find BY
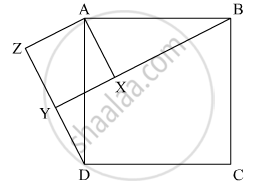
From the above figure we have XY=YZ=AZ=AX
Now in the given figure
DZ = DY + YZ
= 3+2
= 5cm
So,
`AD = sqrt(DZ^2 + AZ^2)`
` = sqrt(25 + 4)`
` = sqrt 29 cm`
Now inn triangle ΔAXB
`BX = sqrt(AB^2 - AX^2)`
` = sqrt(29 - 4)`
= 5cm
So
BY = XY + BX
= 2 + 5
= 7 cm
APPEARS IN
RELATED QUESTIONS
Complete the congruence statement:
ΔBCA ≅?
ΔQRS ≅?
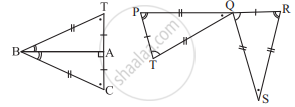
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
State, whether the pairs of triangles given in the following figures are congruent or not:

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
