Advertisements
Advertisements
Question
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Options
True
False
Solution
This statement is False.
Explanation:
Because in the congruent rule, the two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle i.e., SAS rule.
APPEARS IN
RELATED QUESTIONS
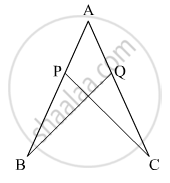
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
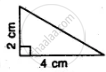
State, whether the pairs of triangles given in the following figures are congruent or not:

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.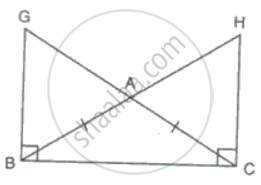
Prove that
(i) BG = CH
(ii) AG = AH
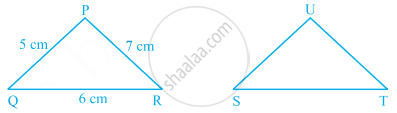
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?