Advertisements
Advertisements
प्रश्न
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
पर्याय
True
False
उत्तर
This statement is False.
Explanation:
Because in the congruent rule, the two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle i.e., SAS rule.
APPEARS IN
संबंधित प्रश्न
Which of the following is not a criterion for congruence of triangles?
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
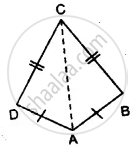
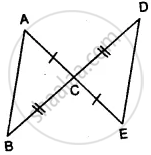
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC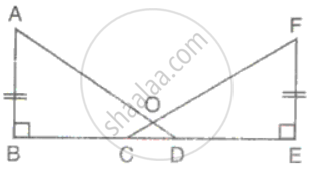
AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.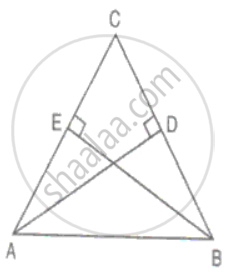
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.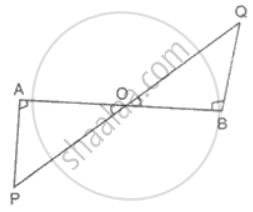
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
The congruent figures super impose each other completely.
