Advertisements
Advertisements
Question
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
Options
BC = PQ
AC = PR
AB = PQ
QR = BC
Solution
If ΔABC ≅ ΔPQR and ΔABC is not congruent to ΔRPQ
Since BC = QR and compare corresponding sides you will see
BC ≠ PQ (As ΔABC ≠ ΔRPQ )
Hence (a) BC = PQ, is not true.
APPEARS IN
RELATED QUESTIONS
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
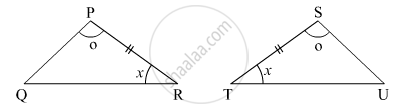
By ______ test
ΔPRQ ≅ ΔSTU
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
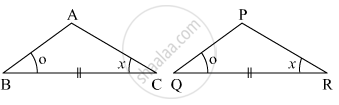
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC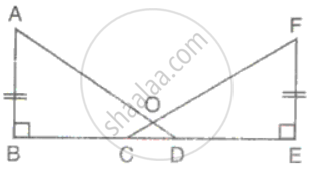
O is any point in the ΔABC such that the perpendicular drawn from O on AB and AC are equal. Prove that OA is the bisector of ∠BAC.
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
