Advertisements
Advertisements
Question
In triangles ABC and PQR three equality relations between some parts are as follows:
AB = QP, ∠B = ∠P and BC = PR
State which of the congruence conditions applies:
Options
SAS
ASA
SSS
RHS
Solution
In Δ ABC and Δ PQR
It is given that
AB = QP
∠B = ∠P
BC = PR
Since two sides and an angle are equal so it obeys SAS
Hence (a) SAS
APPEARS IN
RELATED QUESTIONS
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In triangles ABC and PQR, if ∠A = ∠R, ∠B = ∠P and AB = RP, then which one of the following congruence conditions applies:
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In the given figure, ∠P ≅ ∠R seg, PQ ≅ seg RQ. Prove that, ΔPQT ≅ ΔRQS.

In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.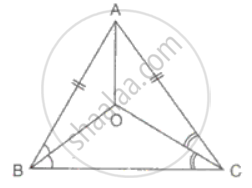
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.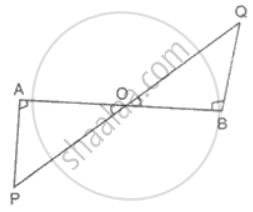
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.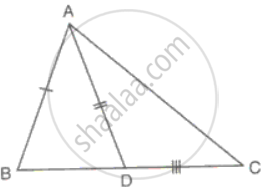
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
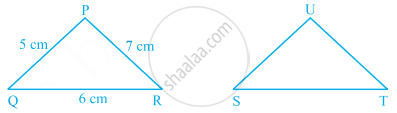
If ∆PQR is congruent to ∆STU (see figure), then what is the length of TU?