Advertisements
Advertisements
Question
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
Options
DF = 5cm, ∠F = 60°
DE = 5cm, ∠E = 60°
DF = 5cm, ∠E = 60°
DE = 5cm, ∠D = 40°
Solution
It is given that ΔABC \[\cong\] ΔFDE and AB = 5 CM . ∠B = 40 , and ∠A = 80°
So AB = FD and ∠C = ∠E
Now, in triangle ABC,
∠A +∠B +∠C = 180°
⇒ 80 + 40 + ∠C = 180°
⇒ ∠C = 60°
Therefore,
DF = 5cm, ∠E = 60°
APPEARS IN
RELATED QUESTIONS
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
If ΔABC ≅ ΔABC is isosceles with
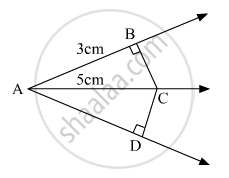
In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD =
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
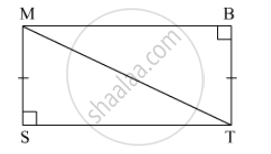
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(BC = 5cm,AC = 6cm,∠C = 80°);
ΔXYZ;(XZ = 6cm,XY = 5cm,∠X = 70°).
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
